| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 디지털트레이닝
- 국비지원교육
- 비전공자
- t-test
- 컴퓨터공학
- 캐글
- 코랩
- 인공지능
- 컨설팅
- 데이터시각화
- 다중회귀분석
- 코드스테이츠
- K-Digital Training
- 빅데이터
- 맥킨지
- BCG
- 주성분분석
- 로지스틱회귀분석
- Ai
- 부트캠프
- 컨설팅펌
- 데이터사이언스
- 웜업
- 파이썬
- AI부트캠프
- 웹스크래핑
- 기계학습
- 선형대수학
- RA
- PCA
- Today
- Total
94년생 스피노자
[노트] 선형대수학 (Vector, Span & Rank) 본문

선형대수학에서 다루는 기본 단위인 벡터를 배워보자.
벡터는 쉽게 말하면 길이와 방향을 가진 선분이다.
그리고 길이는 앞에 특정 수를 곱해서 조절할 수 있다.
간단하게 예를 들어보겠다.
다음 2가지 선택지가 있다고 생각해보자.
- A : 남쪽으로 20 걸음 걷기
- B : 동쪽으로 15 걸음 걷기
여기서 각각의 선택지는 벡터와 같다.
길이(걸음수)와 방향(동서남북)이 주어졌기 때문이다.
앞서 말했듯이 우리는 걸음수를 조정할 수 있다.
0.5*A는 남쪽으로 10걸음 걷기가 되고, -1*A는 북쪽으로 20걸음 걷기가 된다.
만약 우리에게 선택지 A와 B 중 1개 밖에 없다면 어떻게 될까?
A가 주어지면 북쪽 혹은 남쪽으로 밖에 이동할 수 없게 되고
B가 주어지면 동쪽 혹은 서쪽으로 한줄로 이동할 수 밖에 없다.
선택지 A와 B가 모두 주어진다면 무엇이 달라질까?
우리는 지도 속 평면을 모두 갈 수 있게 된다.
동서남북 제약없이 갈 수 있기 때문이다.
1. 2차원 벡터

선택지(벡터) A와 B를 시각화하면 위와 같다.
A와 B의 조합으로 평면상의 어떤 목적지도 갈 수 있다.
선분 A와 선분 B가 서로 선형독립이기 때문이다.
이런 경우 벡터의 Rank는 2가 된다.
벡터의 Rank가 2라는 것은 벡터의 Span이 R2라는 것이고
벡터의 Span이 R2라는 것은 2차원 평면 어디든 갈 수 있다는 것이다.
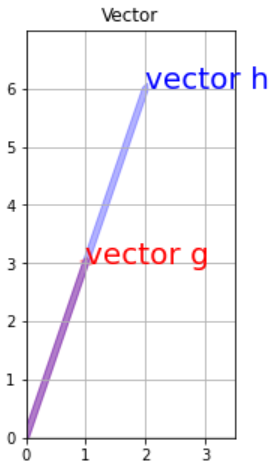
운이 나쁘면 위와 같은 경우도 가능했다.
주어진 선택지의 길이만 다를 뿐 방향은 같은 경우다.
이때 선분 A와 선분 B는 선분종속되어있다고 한다.
결국 우리는 직선 위에서 밖에 움직일 수가 없다.
이런 경우 벡터의 Rank는 1이 된다.
벡터의 Rank가 1이라는 것은 벡터의 Span이 R1라는 것이고
벡터의 Span이 R1라는 것은 1차원 직선으로 움직임이 한정된다는 것이다.
* 벡터들의 Rank를 알아보기 위한 코드
import numpy as np
from numpy import linalg as la
a = [1,3]
b = [2,6]
X1 = np.array([a, b])
print(la.matrix_rank(X1))출력되는 값이 Rank의 값이 되며 동시에 Span이 된다.
2. 3차원 벡터
3차원 벡터에서도 위의 분석 방식은 동일하게 적용된다.
이번에는 동서남북에 더해 위아래라는 방향도 추가됐다고 생각해보자.
주어진 선택지는 아래와 같다.
- L : 북쪽으로 1걸음, 동쪽으로 2걸음, 위로 3번 점프한다. [1, 2, 3]
- M : 남쪽으로 1걸음, 위로 7번 점프한다. [1, 0, 7]
- N: 북쪽으로 4걸음, 동쪽으로 8걸음, 위로 2번 점프한다. [4, 8, 2]

3차원 도식으로 보니 선분독립과 선분종속을 알아보기가 어렵다.
위에서와 마찬가지로 Rank를 구하는 파이썬 코드를 활용해보자.
* 벡터들의 Rank를 알아보기 위한 코드
import numpy as np
from numpy import linalg as la
l = [1,2,3]
m = [-1,0,7]
n = [4,8,2]
X2 = np.array([l, m, n])
print(la.matrix_rank(X2))이때 Rank의 값은 3이 출력된다.
즉 세 선분을 활용해 3차원 공간 어디든 갈 수 있다는 뜻이다.
위 자료는 아래 블로그에서 공부한 것을 바탕으로 작성했다.
참고자료: https://exupery-1.tistory.com/120
모두 행복하길
-끝-
'코드스테이츠 AI 부트캠프 > i) 데이터사이언스 기본' 카테고리의 다른 글
| [Week 3 - Day 4] Clustering (0) | 2021.05.22 |
|---|---|
| [Week 3 - Day 3] Dimension Reduction (0) | 2021.05.21 |
| [Week 3 - Day 2] Intermediate Linear Algebra (0) | 2021.05.21 |
| [Week 3 - Day 1] Vector/ Matrix (0) | 2021.05.21 |
| [Week 2 - Day 4] Bayes Theorem (0) | 2021.05.15 |




